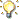GRV: Lavillenie - From Stall Swing to World Record

[KirkB]

What other recent, non-obvious discoveries have we made regarding RL's technique, that are distinctly different than SB's, and are NOT mere style differences?

There are other many other style differences between SB and RL, many of which are due to the tuck/shoot aspect of RL's technique that's absent in SB's technique.

One of these is the emphasis on RL's strong bottom arm, whereas SB has little or no bottom arm pressure. This is obvious from his vids (although whether SB used his bottom arm or not has been the subject of much debate on PVP).

But this is a difference between the PM and the tuck/shoot method, not any difference that can be specifically noted as a new or novel technique that RL does (any different than any other tuck/shooter).

It's just that he does it better.

So again (getting back on topic), are there any other recent, non-obvious discoveries that we made regarding RL's technique, that are distinctly different than SB's, and are NOT mere style differences?

Kirk

[PVstudent]

Jean Galfione and Kory Tarpenning Paris 1996
http://youtu.be/Q3D_vujPqRI

The video is not without some irony with respect to recent debate on style and technical necessity. French vaulter using an effective lead leg action at take-off and USA vaulter little to no effective lead leg action. Both vaulters were arguably great technicians of their day.

Guissepe Gibilisco World Champion 2003 Sequence 1.jpg (92.14 KiB) Viewed 20797 times

Guissepe Gibilisco World Champion 2003 Sequence 2.jpg (89.43 KiB) Viewed 20797 times

Tuck and shoot is not a stylistic difference. Nor can it be considered as NOT possible within the Petrov - Bubka Method of Pole Vault training Technical Model!

Guissepe (Pepe) was developed by Vitali Petrov and became World Champion 2003.

I have never heard Vitali Petrov say or suggest that a vaulter must not tuck and shoot if it is necessary to complete the vault.

My understanding is that he regards the tuck and shoot method as having mechanical disadvantages that prevent a vaulter from fully exploiting the amplitude and power of the long leg swing that can be developed as a result of the free take-off. It also makes difficulties for the vaulter in staying close to the line of recoil thrust force from the pole whilst executing the turn into the push off at pole release.

Tuck and shoot is necessary for some vaulters to safely complete the attempt but it is much less efficient in executing the "spiral turn and push off" that completes the second phase of pole support.

Tuck and shoot becomes a technical necessity for some vaulters to enable them to "cover the pole" in time and simultaneously obtain a body segment arrangement with respect to the pole that optimises their capacity to use the pole recoil without stalling the total system at a horizontal and vertical location that is too far in front of the vertical plane of the cross bar to make the attempt with sufficient margin of safety and continue the vault to completion.

[Tim McMichael]

Tuck and shoot is necessary for some vaulters to safely complete the attempt but it is much less efficient in executing the "spiral turn and push off" that completes the second phase of pole support.

But Lavillenie comes from as extreme a tuck and can be imagined. It can't be "much less efficient," can it? I have said this before on this forum, but I'll say it again here. Tucking from a long and powerful swing does not rob the vault of energy. The law of conservation of angular momentum still applies. Gong from long to short speeds up the rotation but does not diminish the power of the swing. What it does do is allow the athlete to stay low and behind the pole longer. A lower center of gravity in the first part of the jump is never a bad thing.

[altius]

APOLOGIES FOR THE CAPS TIM - YOU KNOW I AM NOT SHOUTING AT YOU - JUST TECHNOLOGICALLY CHALLENGED! First let me repeat my belief - supported by a certain amount of evidence - that had Bubka set the record at the unapproachable level he was capable of, this whole discussion would never be occurring. But I know that statement will just vanish into the ether so dont worry about it!

Tucking from a long and powerful swing does not rob the vault of energy. TIM IS THAT A FACT OR AN OPINION? WOULD LIKE TO SEE THIS CLARIFIED IN TERMS OF THE BIOMECHANICS The law of conservation of angular momentum still applies. Gong from long to short speeds up the rotation but does not diminish the power of the swing. IS THAT A FACT OR AN OPINION - JUST THOUGHT THAT MAY OR MAY NOT BE RELEVANT - I KNOW ENOUGH ABOUT HAMMER THROWING TO KNOW THAT A HAMMER THROWER WOULD NEVER ATTEMPT TO SPEED UP THE ROTATION BY SHORTENING THE RADIUS OF THE SWING. What it does do is allow the athlete to stay low and behind the pole longer. HOW DOES SPEEDING UP THE ROTATION ALLOW THEM TO STAY LOW AND BEHIND THE POLE LONGER - I UNDERSTAND THE LOGIC THAT IF YOU KNOW YOU CAN GET UP SIDE DOWN FASTER YOU CAN AFFORD TO STAY DOWN LONGER - BUT IF THIS IS NOT CLARIFIED IN VERY SIMPLE TERMS IT WILL CERTAINLY BE MISUNDERSTOOD BY MANY COACHES - AND ALONG WITH THIS STATEMENT = A lower center of gravity in the first part of the jump is never a bad thing.[/quote] MAY TAKE US BACK TO THE BAD OLD DAYS WHERE THE AIM WAS TO BEND THE POLE AS MUCH AS POSSIBLE BEFORE LEAVING THE GROUND - SOMETHING LAVELLENIE DOES NOT DO - AND TO TAKE OFF UNDER - AGAIN SOMETHING THAT HE DOES NOT DO.

However what really bothers me is the question of how you teach vaulters to jump like this in safety? With the Petrov Bybka model it is easy to take an absolute beginner forward in safety with a technical model that will be valid from their first take off until they break the world record. As I am primarily just a teacher, for me that is the critical question that trumps all of the above debate.
So as a ps I am still hoping to meet D'auncausse and Lavellenie in Zurich and ask them to clarify these issueS for me. If it comes off I will let you know.

[Tim McMichael]

However what really bothers me is the question of how you teach vaulters to jump like this in safety? With the Petrov Bybka model it is easy to take an absolute beginner forward in safety with a technical model that will be valid from their first take off until they break the world record. As I am primarily just a teacher, for me that is the critical question that trumps all of the above debate.

Thank you, Alan, I’ve been working on these questions, and as usual, it’s taking me longer than I had anticipated, so let me tackle them one at a time. The last objection is the most important, and I could not agree more. Safety is paramount, and a smooth, gradual learning curve is the beauty of Petrov’s method. Your book proves this beyond any rational objection. It’s certainly true that the method that I was taught which emphasized staying low and behind the pole was not taught safely. Mr. Dial just kept putting bigger and bigger poles in my hands and saying, “Use this one or go home.” The few of us who were able to do this had long and successful careers. Those who didn’t quit. But it’s a miracle nobody got hurt. We relied a lot on faith back then and I remember thinking more than once that I might die doing what I love. This is not acceptable, and I would personally abandon any method, no matter how successful, that put athletes in danger. I believe I am in the process of discovering how to teach this method safely and I owe that fact to your exposition of Petrov’s ideas. I can’t be as detailed as I would like because this is in process for me, but the rough outlines of what I am working on are taking shape.

The main reason that this method isn’t safe is that it can be so easily misinterpreted and misapplied by athletes and coaches. If all you are emphasizing is staying behind the pole in the first two thirds of the vault, athletes are going to run badly, takeoff under, and jam their bottom arm through the pole and the whole sport then takes a huge step backwards. What I am finding is that if I teach Petrov’s methods regarding the approach and takeoff first and THEN work on staying behind the pole the result is a vault that is fundamentally safe. The learning curve is still pretty steep because the timing involved in a proper tuck is very difficult, but failures still end up in the middle of the pit. This progression also lets me evaluate which method will work best for an individual athlete. If a developing vaulter appears to be doing just fine with a high takeoff and a long swing, I can leave it alone and let their vault grow from that foundation. However, if an athlete appears to have the instinct to keep their center of mass lower and then tuck, I can teach that too. I am well aware that one paragraph is by no means a complete explanation, nor am I anywhere close to done working on this problem, but I at least want to give you some assurance that I haven’t lost my mind and that safety is still first with me as it should be with us all. And that is as close as I will probably get to an absolute dogma.

[altius]

Now in Oregon City with Rick Baggett.

As always rational and considered Tim - very sane! The sort of thing that really does enhance our understanding of how to help young people begin to become better vaulters.

Not sure if you have looked at the film of the young girl I have posted in the beginners section. The presentation is pretty basic but she represents how I believe one should teach the vault; I will try and send film of her progress as she naturally moves to bending the pole and learns to invert. In addition – if I live long enough - I will post film of the three girls we have in the 13/15 age group, whom I believe will all jump 3.50 – 3.70 in December at our national schools championships. I think that they will clearly show how it is possible for athletes to use the same recognizable technical model – based on Petrov – but still have minor differences that reflect their individuality.

Finally if anyone gets to the World Juniors in Eugene in late July they will see another one of our athletes in Kurtis Marschall. He has improved from 4.05 to 5.05 in around 15 months but on the basis of his last training session I am dreaming –yes coaches dream too! – that he could jump 5.30 . He is one of our latest attempts to apply the Petrov model to ordinary young athletes..

[altius]

"With the Petrov Bubka model it is easy to take an absolute beginner forward in safety with a technical model that will be valid from their first take off until they break the world record."

I am very conscious of the fact that I will be told that this is off topic - but if this occurs I will disagree because the above sentence is critical to OUR approach to teaching and coaching this event. Some readers may know of my deep interest in military history so one of my favourite quotes is one by Napoleon who said, "Every soldier carries a Field Marshalls baton in his pack." These were not just empty words, because many of his most famous generals did start out in the ranks of the revolutionary army.

As a teacher I liked this philosophy so much that it has come to underpin my whole approach to teaching sports, including the pole vault. So every athlete we meet must be seen as a potential star and at the very least be taught to vault in a way that COULD take them to the pinnacle of success - if of course they have the dedication, physical and mental abilities and the support in all the other areas that are needed for any vaulter to achieve their potential. They will then progress steadily without the 'four steps forward and three back' which is typical of the situation for many young athletes in the US as they meet a myriad of different approaches - I won't call them technical models - as they continue in the sport.

I had hoped that exposure to the logic and effectiveness of the Petrov/Bubka model would by now have convinced the majority of coaches to try to apply it, but unfortunately many still prefer to complicate what is a relatively simple event for reasons even they probably do not understand. Perhaps it makes them feel superior -because they feel they possess esoteric knowledge - or simply because people are prepared to pay more for something that appears to be arcane rather that simple.

The real challenge of coaching is not understanding the technical model but gaining the intuitive knowledge you need to deal with other issues, for example the problems associated with providing advice to any athlete on any given day in any specific set of conditions about which pole to use, where to place the standards, whether to modify the run up, grip height, pole stiffness -what starting height, what progression etc. - and of course how to deal with a situation spiralling towards disaster as the athlete faces a third attempt at the opening height in a competition they are favourites to win. A situation we faced twice this year at our nationals. But this real world rarely if ever gets discussed, so I have concluded that either US coaches are experts in this area already, or on the other hand, many don't really do enough actual coaching to know what the problems are.

Just the ramblings of an old man suffering from jet lag! Changed my mind - in retrospect definitely off topic.

[Tim McMichael]

Tucking from a long and powerful swing does not rob the vault of energy. TIM IS THAT A FACT OR AN OPINION? WOULD LIKE TO SEE THIS CLARIFIED IN TERMS OF THE BIOMECHANICS The law of conservation of angular momentum still applies. Gong from long to short speeds up the rotation but does not diminish the power of the swing. IS THAT A FACT OR AN OPINION

First let me say that I am not a physicist. Compared to some on this board I am a rank amateur. Please forgive me if my language is less than technically precise.

The law of conservation of angular momentum isn't a matter of personal opinion. As far as I know, it's a physical law that applies to all rotating objects. I can't claim to anything original here beyond some insights into how it may apply to the vault. I learned most of this from Joe Dante and Len Elliott's excellent book, "Four Magic Moves to Winning Golf." In it they show how a golfer's hands get further from their spine from the top of the swing to the moment of impact. This means that the arms have to slow down. Nothing can prevent it. The energy has to go somewhere, so it feeds into the club head. Their point is that the late hit that so many golfers fail to attain will happen automatically if they can inhibit the instinctual desire to try to hit the ball. Physics will take over if they let it. The arms will slow as they approach the ball, no matter how powerfully they swing, and the club head will catch up to the hands automatically. I thought about this for a long time as I tried to see how this would apply to the vault which has a double axis, both the vaulter and pole rotating to vertical.

As I understand it, the law of conservation of angular momentum is a description of the way energy is expressed in terms of velocity when an object is rotating around a fixed axis. The smaller the radius of an object, the faster it will rotate given that the energy that set it in motion is a constant factor. The classic illustration is a figure skater performing a spin. If they start with their arms outstretched they will rotate slowly. As they pull their arms in, the speed of the spin increases until they become a blur of motion. The energy, however, remains a constant except what is lost to friction.

Those who believe that tucking is detrimental are thinking about the fact that a long lever rotating around a fixed axis is more powerful than a short one. This is true as far as it goes. The mistake is that they are thinking about the swing as though it proceeds at the same speed all the way to vertical. There is, however, a point at which it reaches maximum speed. This happens when there is a straight line between the vaulter's top hand and the foot of their trail leg.



After this point, the swing begins to fight gravity and will slow down. The more powerful the swing is when it reaches this point of maximum speed, the slower it will decelerate as the swing progresses, but it will begin to lose energy. So, going back to the thought experiment of the figure skater; they put as much energy into the the spin as they can at the start. After the initial push off the ice, no more energy can be added; the spin is gradually slowing due to the friction of the ice from this point onward. By drawing the arms in, they speed up, but the energy that remains is conserved. The spin retains its gradually decreasing power whether they are spinning with a wide radius with the arms outstretched or with a short radius with the arms drawn in. Because, like the figure skater, a vaulter's rotation begins to lose power as it progresses, nothing is lost by tucking provided that the tuck happens after the swing reaches the point of maximum speed. Any shortening of the body before this point would be disastrous. This can be a very bad habit and I have seen it plague many beginners. I think it mostly happens when a well intentioned coach (mistakenly thinking they are teaching what Bubka did) emphasizes getting upside down above all else. The vaulter who has a poor run and takeoff and thinks that getting inverted is the holy grail of pole vaulting finds a shortcut to that goal. They fold their trail leg up at the start of the swing because it takes less initial power to rotate that shorter radius to vertical in time. They do get upside down but with a very weak vault, and if they fold the leg up more than they normally do, they are liable to land in the box.

The other implication of this law as it applies to the vault has to do with style differences among accomplished valuters. If the primary way the vaulter is creating energy through the middle of the vault is with the speed of their swing, the amount of power they are able to produce will influence whether or not they have to tuck. Someone like Bubka will tuck very little or not at all. This is because the swing is moving so powerfully that they are able to catch up to the timing of the pole without needing to speed up their rotation. Someone like Gibilisco may need to tuck because they don't have the same energy in their swing. Or if they do have the power, the tuck adds nothing and subtracts nothing, but it is an unnecessary complication that they could do without.

This is why tucking is seen by so many excellent coaches as universally bad. They observe that great vaulters who use Petrov's method tuck very little or not at all. And very many awful vaulters tuck at the very start of their swing. This, however, renders Lavillenie's vault a mystery without a solution. He tucks as much as he possibly can and is now the current world record holder. I believe this is because the primary way he conserves energy in the middle of the vault is by lowering his center of mass after takeoff and staying low on the chord of the pole as long as he can. But that's the subject of another post.

JUST THOUGHT THAT MAY OR MAY NOT BE RELEVANT - I KNOW ENOUGH ABOUT HAMMER THROWING TO KNOW THAT A HAMMER THROWER WOULD NEVER ATTEMPT TO SPEED UP THE ROTATION BY SHORTENING THE RADIUS OF THE SWING.

The reason hammer throwers should not pull their arms in is because, if they throw correctly, they are constantly pushing against the ground and their rotation is gaining energy all the way to the release of the hammer. It never slows down and the longer lever is more powerful. Even if this were not true; let's say a figure skater released a hammer in the middle of their spin. (I would pay to see that.) Nothing would be gained by shortening the radius. The spin would speed up, but no additional power would be generated. The hammer would leave their hands with the same force whether they were spinning fast with their arms pulled in or spinning slow with their arms outstretched. I suspect that the reason many poor hammer throwers do pull their arms in is because it's easier to get around the ring, much like the vaulter who tucks at the start of their swing.

Anyone who wants to test this out can do it in a swivel chair. (I just did this in my office and my wife is rolling her eyes at me.) Start spinning as fast as you can and stretch your arms out then pull them in. The chair will spin slower and accomplish fewer rotations with the arms outstretched. It will speed up and rotate more times with the arms drawn in, but it will stop spinning at almost exactly the same time every time you do it if you start the spin with the same amount of force.

[Tim McMichael]

let's say a figure skater released a hammer in the middle of their spin. (I would pay to see that.) Nothing would be gained by shortening the radius. The spin would speed up, but no additional power would be generated. The hammer would leave their hands with the same force whether they were spinning fast with their arms pulled in or spinning slow with their arms outstretched.

I have a horrible suspicion that I'm missing something here. But I can't figure out what it is.

[KirkB]

I have a horrible suspicion that I'm missing something here. But I can't figure out what it is.

Not sure if this helps, Tim, but there would be distinct differences between a figure skater with and without a hammer on the end of a cable.

The main difference is the location of the CoG. Without, the CoG is aligned with the skater's spine (more or less). With, the CoG is perhaps halfway between the skater and the heavy ball. I'm not sure why I say halfway - because the hammer weighs 16 pounds (7 kg), yet the skater would weigh at least 150 pounds (68 kg). So you would think the CoG would be closer ot the athlete's body. Yet when you swing a hammer it FEELS like the CoG is quite a ways out from the body.

Secondly, a hammer thrower doesn't rotate around the CoG at an even speed (or even a constant acceleration) - mainly because the hammer doesn't spin at an even distance above ground. So the up-and-down cadence of the rotating ball causes difference forces against the athlete's body at different points in each rotation.

Also, a hammer throw shortens the radius just before the release, doesn't he? He does this by his final 'pull', doesn't he? (I'm not sure). And this speeds things up, doesn't it? And when he does this (if he does), it's against one foot planted firmly in the circle (another fulcrum - in addition to the fulcrum of the spine). This is (contrary to what you're suggesting) to SPEED UP the velocity of the ball, rather than to slow it down.

I don't have the answer for you, Tim, I'm just suggesting a few differences that might lead to some further enlightenment. But maybe not. I haven't studied any other events like I've studied the physics of the PV, so I could be way off.

Maybe Altius can correct both of us, since he's studied the hammer?

And yet ...

I KNOW ENOUGH ABOUT HAMMER THROWING TO KNOW THAT A HAMMER THROWER WOULD NEVER ATTEMPT TO SPEED UP THE ROTATION BY SHORTENING THE RADIUS OF THE SWING.

Kirk

[PVstudent]

Tim your comments on conservation of angular momentum are substantially correct with regard to the ice-skater example as you describe it! Yes ,you have made a an important omission with respect to its analogous application to pole vaulting.

The examples of the ice skater and the hammer thrower have entirely different objective end goals.

The ice skater conserves angular momentum due to shortening the radius of gyration about a perpendicular axis to speed the rate of spin in the horizontal plane of motion. By extending the arms horizontally the rate of spin decreases accordingly. There will be some small loss of angular momentum overall due to the opposing frictional force from the ice as the rate of spin firstly increases on drawing the arms (adducting) closer to the axis of rotation and slows down on the lateral abduction of the skater's arms.

The objective of the hammer thrower is to accelerate the mass of the hammer to achieve maximum tangential (linear) velocity on release as a result of angular momentum developed about a perpendicular axis to the plane of motion of the hammer. This is not a horizontal plane of motion and is therefore unlike that of the ice skater example. The linear or tangential speed of the hammer is increased when the rate of spin is kept constant and or increased as the radial distance from the axis to the centre of mass of the hammer lengthens. Hence the hammer thrower lengthens the radius of hammer head gyration to achieve greater magnitudes of the linear release speed.

But neither the ice skater nor the hammer thrower confront the challenge facing a pole vaulter!

The ice skater's motion is in a horizontal plane about a vertical axis. The angular motion of the hammer throw is in a plane at varying inclined angles to the horizontal plane of motion of the thrower's feet.

The pole vaulter must rotate themselves and the pole about two primary horizontal axes perpendicular to a vertical plane of motion as well as about a vertical axis to the horizontal plane during the inversion spiral turn. In the pole vaulter's case the primary challenge is to produce angular momentum sufficient to rotate the total system about these axes in opposition to angular momentum due to gravitationally induced torque acting for almost the entire pole support phase of the vault.

Because the vault rotation challenge is rotation predominantly in the vertical fore - aft (sagittal) plane the role of gravity and hence the weight force induced torque critically affects the outcomes of conservation of momentum influences on the motion experienced by the vaulter and perceived by the external observer.

Contrary to the assumption that resisting frictional forces are minimally influential in the pole support phase of the vault, friction forces can and do dramatically influence the efficiency of the elastic recoil transfer effect on the vaulter.

Also, since the path of the total system in pole vaulting in curvilinear the momentum or energy exchanges have to considered in very small units of time or displacements ,or both, to accurately account for the observable outcomes.

It is impossible for any pole vaulter to actually physically violate the conservation laws established by physicists!

Many interpretations of how these conservation laws apply in pole vault are indeed subject to fallibility.

[PVstudent]

A preliminary examination of the pole support phases from first to second take-off has to be made to keep this discussion based on universally understood mechanical and biomechanical definitions and concepts.

These concepts can then be properly applied to pole vaulting in general as well as to an analysis of the specific vaulting techniques used by Sergei Bubka and Renaud Lavillenie.

The analysis is limited to being merely qualitative because reliable, scientifically obtained quantitative data on the two vaulters in question are not readily available in the public domain. This is particularly the case for the most recent performances of the technique currently (2014) used by Renaud Lavillenie.

Unravelling “beliefs” in regard to the way in which “conservation laws” (of energy or momentum) operate in this vital part of the total vault process necessitates keeping the discussion focussed on accurate descriptions that can be universally accepted and understood as being supported by both physical mechanical laws and very strong empirical evidence. Of equal importance the “face validity” of claims and assertions in regard to the technique currently used by Renaud Lavillenie in 2013 -2014 need to be evaluated.

Qualitative video / film evidence from the recorded images of pole vault performances by both Bubka and Lavillenie is readily obtainable from the analysis of recordings obtained from internet sources and forms the major source of technique performance evidence upon which my contribution to this discussion will be based.

What follows in this and some additional posts is an attempt to assist readers and myself in clarifying conceptual understanding of the pole support phases of the vault and to propose a mechanics based rationale to account for the relative successes of PB (Petrov-Bubka Technique: specific to Sergei Bubka) and the technique termed “Tuck and Shoot” specifically performed most recently (post 2012 Olympic Games to July 2014) by Renaud Lavillenie.

Local and remote axes of pole rotation top hand and pole tip respectively.jpg (66.13 KiB) Viewed 20200 times

First some definitions and explanation of the diagram above.

Diagram definitions:
1st take-off, foot / toes of the take-off leg breaks contact with the runway surface) instant 1.

2nd take-off, the first observable instant when the vaulter having completed the inversion spiral (approximate) 180 degree turn about the local axis of the vaulter’s the upper grip location length along the pole is released and the vaulter commences flight at instant 8 in the drawing).

Curvilinear pathway, the actual path followed by the vaulter’s centre of mass (COM) resulting from non-uniform motion with combining rotation and translation. The pathway is indicated by the dashed black curve traced out during the motion sequence by the vaulter’s COM.

Radius L, the radial distance from the top of the top grip on the pole to the centre of mass of the vaulter.

Radius R, the radial distance from the vaulter’s centre of mass (COM) to the pole tip located at the deepest location in the planting box.

+M, the anticlockwise moment about a local or remote X,Y,Z rotation axis.

-M, the clockwise moment about a local or remote X,Y,Z rotation axis.

Numbers on the diagram, refer to the body segment configuration and COM location at selected instants in time during the pole support continuous action sequence from take-off to final pole release by the top grip hand.

Diagram Explanatory Notes:

1. The diagram drawings were made from film of Sergei Bubka and represent “snapshots” at selected instants in the continuous action sequence of the pole support phases of the vault. The pathway of the vaulter’s COM was determined from cine film using frame by frame segmental analysis method. The pathway COM XY coordinates from all the still frame images were plotted on to the frame by frame images and transposed to the diagram made from copying the images by means of contour drawing. The resulting XY plot was smoothed and transferred to the selected image diagram shown above.

2. At instant 1 the toe tip is breaking ground contact at take-off following the completion of the pole plant that linked the approach run and pole carry and take-off foot ground contact.

Note the relative location of the top grip hand to the vaulter’s COM which is moving forward and upward in the same plane (XY) at the instant the take-off toe breaks ground contact. The COM is well in advance of the position of the top hand as take-off occurs. The full implications of this fact will be elaborated in my next post.

3. The Green Cross circle is located at the position along the pole of the top hand grip. The straight line linking this point to the vaulter’s centre of mass (COM) Radius L1 is the radial distance from the vaulter local axis of rotation (transverse horizontal axis) to the vaulter’s COM. Note the height of the vaulter COM and its horizontal distance in advance of the take-off foot toe tip.


4. The vaulter’s COM , Black and Yellow Cross Circle, has a Radius R1 from the pole tip (Remote Axis: transverse horizontal (Z) axis at take-off with the understanding that at the pole tip rotation has multiple axes throughout the course of the pole support phases).

5. The dashed (black) curve is the 2-D smoothed curvilinear pathway in the XY plane of the vaulter’s COM.

Note firstly that this indicates that the rise (vertical elevation) rate of the COM varies throughout both bending and recoil phase of pole support. The rise rate rapidly increases just before maximum pole bend and continues this positive rise rate until about instant 7. The COM rise rate then decreases during the lower hand pole release from instant 7 and final pole release occurs at instant 8. After this instant the vertical rise is subject to a constant acceleration in the negative y direction and the vaulter is in post 2nd take-off flight ascent phase until peak flight height of the COM is reached.

6. The curvilinear pathway of the COM during the bending of the pole reveals that the vaulter’s muscular effort and momentum transfer to it, is dominated by the resultant tangential forces and torques.

Note the vaulter induced forces / torques and the speed at which they are generated (Power) dictate the rate and amplitude of pole bending in the 1st Pole Support Phase depending upon the elasticity characteristics of the pole selected for this particular vault.

The total system COM horizontal displacement forwards towards the plane of the crossbar, due to the associated pole bending and lateral “snap deflection,” carries the total system centre of mass more rapidly horizontally forward compared to its speed of vertical ascent. This is confirmed by the change in slope of the vaulter’s COM curvilinear pathway depicted on the diagram from instant 1 to just about instant 3.
After this point in time the rate of COM rise climbs rapidly until about instant 5 when the vaulter’s clockwise (-ve) rotation about the top grip and mid shoulder axes has enabled both lower limbs to align approximately parallel with the upper and lower grip section of the pole (“covering the pole”).

The “swinging backward - roll up” into maximum pole bend that ends phase one of pole support.

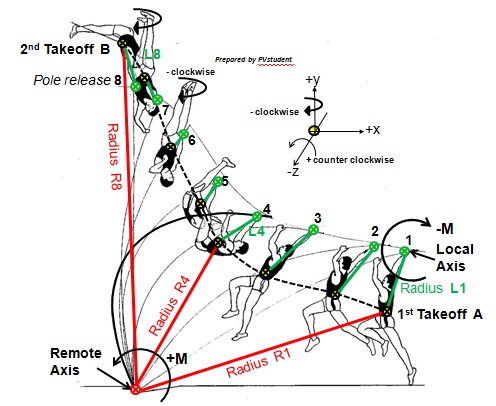
Back roll up to inversion via the secondary mid - shoulder axis.jpg (97.9 KiB) Viewed 20200 times

(My drawings in diagram 2 above were made using the methods previously described. It is taken from a different vault by Bubka and is approximately equivalent to what occurs between instants3 to 4 in the first diagram).

The diagram above illustrates how Sergei Bubka changes his swing rotation axis from primarily about the top grip towards the mid shoulders thereby accelerating the already forced pendular swing to increase the magnitude of the tangential velocity of his COM and of the foot of the swing leg directed vertically upward at about the same time that maximum pole bend occurs.

This subtle rotational axis shifting creates an increase in linear tangential velocity of the vaulter’s COM about the top hand and at the same time produces a very large increase in the magnitude of the vertical momentum component that is coincident in time and direction with the start of the pole recoil impetus applied to the vaulter.

This axis shift may also slightly increase the duration of the time during which the vaulter is able to maintain and or apply additional muscle generated torques to accelerate the extended leg swing whilst at this same time gaining additional arc length travel distance in the swing.
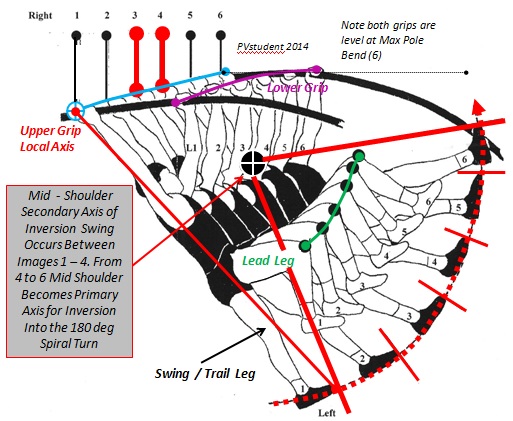
Tangential Velocity (m/sec) is angular velocity (rads/sec) multiplied by length of the radius in metres. Angular momentum is moment of inertia (mass (kg) x radius (m) x radius (m)) multiplied by angular velocity (rads/sec).

Lengthening the leg swing radius without losing angular velocity will result in a proportional increase in linear tangential velocity.

In the Bubka vaulting sequence shown below maximum angular momentum occurs around the snapshot instant depicted in image 13 and the maximum foot tangential velocity occurs during maximum pole bend and the start of pole recoil. The path of the hips (black cross circle) is predominantly vertical upward from maximum pole bend until the start of the inversion turn at instants 20-21.

Bubka Dijon Petrov Model.jpg (70.01 KiB) Viewed 20200 times

Thus the advantage to this form of inversion swing is that the momentum vector direction of the vaulter’s COM and that of the pole recoil impulse (average recoil force x time) are parallel and both act simultaneously in a primarily upward direction.

The vertical velocity component of the vaulter’s COM reaches a peak close to the time at which pole chord lengthening is coincident with the longitudinal axis of the pole (recoiled fully to its un- flexed resting length).

This is due to the conservation of angular momentum about the local axis of rotation being coupled in time and spatially coordinated with the pole recoil force vertical component to cause the vertical rise of the COM in the curvilinear pathway from the instant of radius length L4 until L8 when pole release occurs as shown in diagram 1.

This effect is further enhanced by the vaulter’s straight inverted body held in firm alignment with the vaulter’s longitudinal axis and maintained in close proximity to, and in parallel with, the rotational displacement of the chord and longitudinal axis of the pole during pole recoil.

7. Previous discussion in this thread has focussed attention on the conservation of energy or momentum of the vaulter but has not clearly elucidated how this is used to continue propulsion of the total system about the remote pole tip axes located in the planting box.

Diagram 1 shows the relative changes in radial lengths from the vaulter’s COM to both the local and remote axes of rotation.
COM to Local Axis is Green Line L1-L8.
COM to Remote Axis is Red Line R1 – R8.

Note in reviewing diagram 1 the vaulter COM radius (L) shows a decrease in length from take-off until about instant 6 after which it slightly increases in length until pole release L8.

(a) From take-off, until about instant 6 and the start of the vaulter’s half turn, the rotation of the vaulter is in a clockwise direction. This is opposite to the anticlockwise direction of the total system rotation about the pole tip.

(b) The vaulter rotation direction about the local axis at the top hand grip is changed by the 180 degree turn in combination with the spiral movement upward such that the vaulter’s COM passes above the level of the top grip. At about the time this occurs the vaulter’s COM rotation becomes concordant in direction (+ve anticlockwise) with that of the pole chord about the pole tip remote axis in the deepest point of the box.

8. The COM to the Remote Axis Radius (R) needs to be examined carefully in relation to the changing moment of inertia of the vaulter’s COM with respect to this axis and the curvilinear pathway during both phases of pole support.

Note the radial distance (R) of the vaulter’s centre of mass to the remote pole tip axis is shown clearly in the diagram to be a major determinant in creating the potential for “stalling” the anticlockwise rotation of the total system about the pole tip.

This stall potential is reduced when the “approximately 180 degree spiral turn” is completed quickly and an additional “torque couple” is created by the vaulter that acts in the same direction as the total system angular momentum.

The vaulter achieves this desired outcome by means of a “ pumping a playground swing type action” around the vaulter’s top grip fulcrum timed to adds some angular momentum to rotation around the pole tip even though the radial length R to the vaulter COM is increasing.

[i]The timing of the directional change of vaulter angular momentum is critical to successfully lowering the rate at which vertical velocity decreases whilst the total moment of inertia of the system about the remote axis is getting larger from maximum pole bend to pole release.

The radial length R increase from maximum pole bend to pole release is revealed to be much longer than the reduction in length of radius R from take-off to maximum pole bend.

The following posts will address these considerations in more detail.

In the next post I will first discuss the challenge posed by the moments of force (torques) opposing vaulter muscular effort. I illustrate the fact that the vaulter weight force (-mg) induces varying magnitudes of the torques that the vaulter must overcome by swing power and swing amplitude in conjunction with vaulter controlled specific body actions (especially of the shoulders and hips).

Vaulter whole of body segmental configurations and alignment with respect the top hand grip local axis (Z) and the longitudinal axes (Y) of both the vaulter and the pole will also be explained.

Secondly I will propose some advantages that can be gained from the whole body “inversion and longitudinal turn technique employed by Bubka” which is based on the application of Principles of Raising an External Weight by Turning a Helical Screw Between Two Relatively Fixed End Load Bearing Points to cause vertically upward linear translation of an external object (the vaulter).

Attempting to unravel the how and the why the inversion into the turn is mechanically effective in what I define as the Helical Screw Turn Model of Using Vaulting Pole Recoil (PB Technical Model as demonstrated by Bubka) in contrast to the equally effective use by Renaud Lavillenie of what I define as a “Trebuchet Type” Underswing Toe Shoot with Half Turn Model of Using Vaulting Pole Recoil, I will share evidence to reveal that Renaud Lavillenie's 6.16m (indoors) vault is not an enigma.